Nos ponemos técnicos, muy técnicos, aunque sin ahondar en muchos detalles ya que éstos son propios de las ciencias de la computación y matemática, sin embargo sí trataremos una buena parte del conocimiento que nos atañe como desarrolladores de software.
Usualmente hacemos algoritmos sin preocuparnos mucho del coste de procesamiento que va a tener, salvo que hayamos caído en algun diseño de algoritmo muy ineficiente en donde sí, en efecto, nos preocuparíamos y trataríamos de refactorizarlo o hacerlo más eficiente, pero como decía antes, no es común que nos preocupemos de estas cosas, ya que asumimos que con los estándares de procesamiento de hoy en día, la diferencia en términos de tiempo y procesamiento de un algoritmo a otro es despreciable.
Eso es parcialmente cierto, hoy en día las máquinas, en particular los procesadores, son tan potentes que uno se puede dar el lujo de sacrificar eficiencia de procesamiento por practicidad y rapidez en el desarrollo, pero no hay que abusar.
Crack pero recuerda que este blog es pragmático, es decir brutalmente práctico así que no nos vamos a complicar la vida y tratar de aprenderlo todo, sino sólo lo que nos sirva en la vida real.
Porqué aprender estos temas
Existen dos casos en los que, al menos yo, he notado que sí vale la pena hacer un análisis más profundo de la eficiencia de nuestro algoritmo para poder hacerlo lo más eficiente posible:
- Cuando tenemos cantidades muy grandes de información, y esto es especialmente importante cuando hay bucles, ya que una pequeña diferencia de 5 milisegundos en una sola operación no significa gran cosa, pero iterar eso a 1 millón de registros, supondría más de 1 hora con 23 minutos adicionales.
- Cuando trabajamos con sistemas de tiempo real, aquí tienes un buen tema para que investigues crack.
Existe un motivo más por el cual darle importancia a aprender estos temas, al menos lo básico, y es por las entrevistas técnicas, muchas veces uno responde empíricamente, como se dice, o por descarte 😄 pero nada mejor que saber el porqué de las cosas, además que como pocos programadores saben estos temas, el responder con criterio, te va a subir tus bonos, eso dalo por hecho.
Complejidad de tiempo / Time Complexity
Es la cantidad de tiempo que dura la ejecución de un algoritmo y está estimada en términos de la cantidad de operaciones elementales que se ejecutaron en total.
Pa' tu 📕: Operaciones elementales son en términos sencillos operaciones aritméticas básicas (+-×÷), comparaciones lógicas, acceso a vectores y matrices, asignaciones de variables y similares.
El aprender cómo medir el procesamiento que tiene que realizar un algoritmo en términos de cantidad de operaciones elementales efectuadas por el microprocesador nos ayuda a entender su nivel de eficiencia y tiempo requerido.

Tipos de complejidad temporales
Para entender los tipos tenemos que antes comprender cuál es la notacion de estas complejidades, y la utilizada en estos casos es la llamada Notación O-Grande también conocida como Big-O Notation. En palabras sencillas es una función sólo que en vez de f usamos O.
Recordemos matemáticas un poco y la teoría de Funciones, recuerdan esto?
f(x) = y
Es casi lo mismo sólo que usaremos la notación O, es decir tendríamos:
O(x) = y
Donde:
x -> cantidad de elementos implicados en el algoritmo
y -> la cantidad de operaciones realizadas
Con cantidad de elementos implicados me refiero a por ejemplo la longitud de un arreglo al cual vamos a aplicar un bucle
Con cantidad de operaciones elementales me refiero a la cantidad de iteraciones que habrá en ese bucle, suponiendo que en cada iteración se realiza una sola operación.
Veamos cada tipo de complejidad y un ejemplo de código por cada una:
Tener en cuenta que el tiempo de duración de los algoritmos que veremos a continuación están expresados en milisegundos
Constante
Su notación es O(1)
Este tipo de complejidad se da en los algoritmos en los cuales sin importar la cantidad de elementos implicados, el número de operaciones efectuadas en el mismo es el mismo.
El siguiente algoritmo presenta una complejidad de notación O(1)
private static void ConstantExecution(int length)
{
var array = populateArray(length);
DateTime start = DateTime.Now;
var first = array[0]; //realiza 1 sola operación
TimeSpan elapsedTime = DateTime.Now - start;
Console.WriteLine($"Elapsed time: {elapsedTime.TotalMilliseconds}\t -> {length} elements / 1 operation");
}
Como podemos ver hemos hecho uso de un método auxiliar llamado populateArray, sólo llena un arreglo con la longitud que queramos, lo usaremos también para comprobar los siguientes ejercicios así que el código es este para que lo tengas en cuenta:
/********************************* AUXILIAR *********************************/
private static int[] populateArray(int length)
{
int[] array = new int[length];
for (int i = 0; i < length; i++)
{
array[i] = i;
}
return array;
}
Y luego probamos varias veces el algoritmo con el siguiente código:
private static void TestConstant()
{
Console.WriteLine("\r\n *** Constant ***");
ConstantExecution(1000000);
ConstantExecution(100000);
ConstantExecution(10000);
ConstantExecution(1000);
ConstantExecution(100);
}
Tenemos estos resultados:

Como podemos observar sin importar el número de elementos del arreglo, el tiempo se mantiene casi constante.
Lineal
Su notación es O(n)
En este tipo de algoritmos la el número de operaciones aumenta de forma proporcional al número de elementos, por lo tanto también el tiempo aumenta de forma lineal.
Veamos un ejemplo con código:
private static int LinealExecution(int[] arreglo)
{
DateTime start = DateTime.Now;
var contador = 0;
for (int i = 0; i < arreglo.Length; i++)//itera por cada elemento
{
contador++;//hace 1 operación por elemento
}
TimeSpan elapsedTime = DateTime.Now - start;
Console.WriteLine($"Elapsed time: {elapsedTime.TotalMilliseconds}\t -> {arreglo.Length} elements / {contador} operations.");
return contador;
}
Y lo podemos probar así:
private static void TestLinear()
{
Console.WriteLine("\r\n *** Linear ***");
int[] arreglo1 = populateArray(1000000);
int[] arreglo2 = populateArray(100000);
int[] arreglo3 = populateArray(10000);
int[] arreglo4 = populateArray(1000);
int[] arreglo5 = populateArray(100);
LinealExecution(arreglo1);
LinealExecution(arreglo2);
LinealExecution(arreglo3);
LinealExecution(arreglo4);
LinealExecution(arreglo5);
}
Luego de las pruebas tenemos los siguientes resultados:

Logarítmica
Su notación es O(Log n)
En este tipo de logaritmos el número de elementos implicados es inversamente proporcional al número de operaciones elementales ejecutadas, es decir mientras hay más elementos, hay menos operaciones, probémosla con código:
private static int LogarithmicExecution(int[] array, int step)
{
DateTime start = DateTime.Now;
var contador = 0;
for (int i = 1; i <= array.Length; i *= step) // va iterando a pasos agigantados porque se multiplica
{
contador++;
}
TimeSpan elapsedTime = DateTime.Now - start;
Console.WriteLine($"Elapsed time: {elapsedTime.TotalMilliseconds}\t -> {array.Length} elements / {contador} operations.");
return contador;
}
Y lo probamos:
private static void LogarithmicTest()
{
Console.WriteLine("\r\n *** Logarithmic ***");
var array1 = populateArray(10000);
var array2 = populateArray(100000);
var array3 = populateArray(1000000);
var array4 = populateArray(10000000);
var array5 = populateArray(100000000);
var array6 = populateArray(1000000000);
LogarithmicExecution(array1,5);
LogarithmicExecution(array2,5);
LogarithmicExecution(array3,5);
LogarithmicExecution(array4,5);
LogarithmicExecution(array5,5);
LogarithmicExecution(array6,5);
}
Tenemos los siguientes resultados:
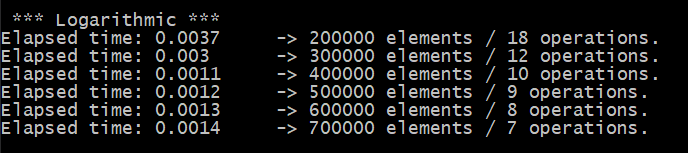
Como notamos en este tipo de complejidad algorítmica el tiempo disminuye a medida que hay más elementos implicados.
Exponencial
Puede ser cuadrática, cúbica, etc, su notación es O(n2) para la cuadrática y así sucesivamente...
Podemos hacer un ejemplo:
private static int ExponentialExecution(int[] array)
{
DateTime start = DateTime.Now;
var contador = 0;
for (int i = 1; i <= array.Length * array.Length; i++) // la cantidad de elementos crece cuadráticamente
{
contador++;
}
TimeSpan elapsedTime = DateTime.Now - start;
Console.WriteLine($"Elapsed time: {elapsedTime.TotalMilliseconds}\t -> {array.Length} elements / {contador} operations.");
return contador;
}
Y la probamos:
private static void ExponentialTest()
{
Console.WriteLine("\r\n *** Exponential ***");
var array1 = populateArray(500);
var array2 = populateArray(1000);
var array3 = populateArray(1500);
var array4 = populateArray(2000);
var array5 = populateArray(2500);
var array6 = populateArray(3000);
var array7 = populateArray(3500);
var array8 = populateArray(4000);
var array9 = populateArray(4500);
var array10 = populateArray(5000);
var array11 = populateArray(5500);
var array12 = populateArray(6000);
var array13 = populateArray(6500);
ExponentialExecution(array1);
ExponentialExecution(array2);
ExponentialExecution(array3);
ExponentialExecution(array4);
ExponentialExecution(array5);
ExponentialExecution(array6);
ExponentialExecution(array7);
ExponentialExecution(array8);
ExponentialExecution(array9);
ExponentialExecution(array10);
ExponentialExecution(array11);
ExponentialExecution(array12);
ExponentialExecution(array13);
}
Los resultados son:
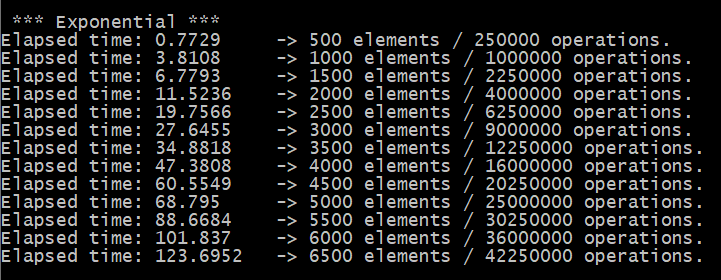
El tiempo aumenta drásticamente a medida que aumentan los elementos.
En resumen
Aquí te presento todos los resultados tanto de tiempo en milisegundos, número de elementos implicados y cantidad de operaciones ejecutadas en los algoritmos para cada uno de los 4 tipos analizados aquí:
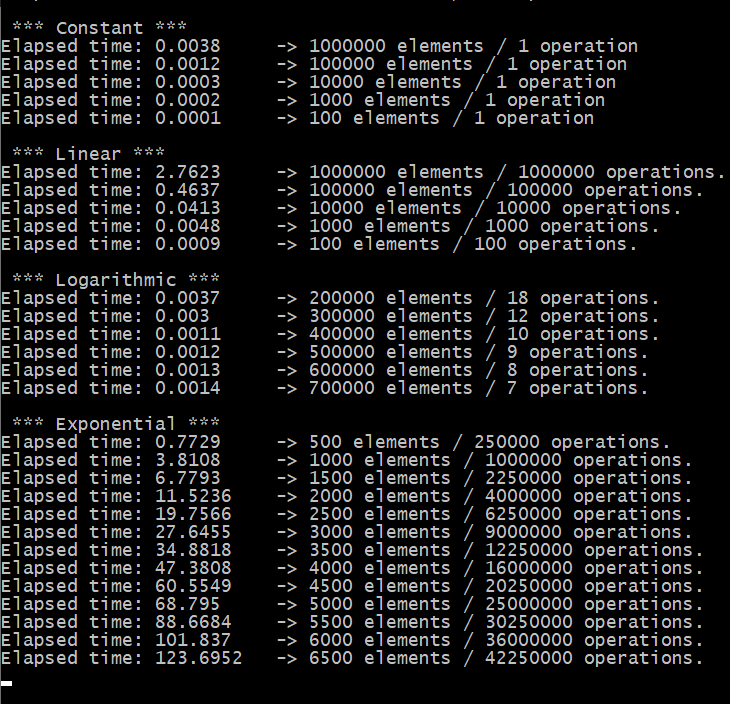
Coloqué esos datos (x e y) e hice unas gráficas de elementos implicados versus cantidad de operaciones y podemos confirmar entonces que los tiempos empleados, en efecto, tienen un comportamiento de una función según corresponda: constante, lineal, logarítmica o exponencial:
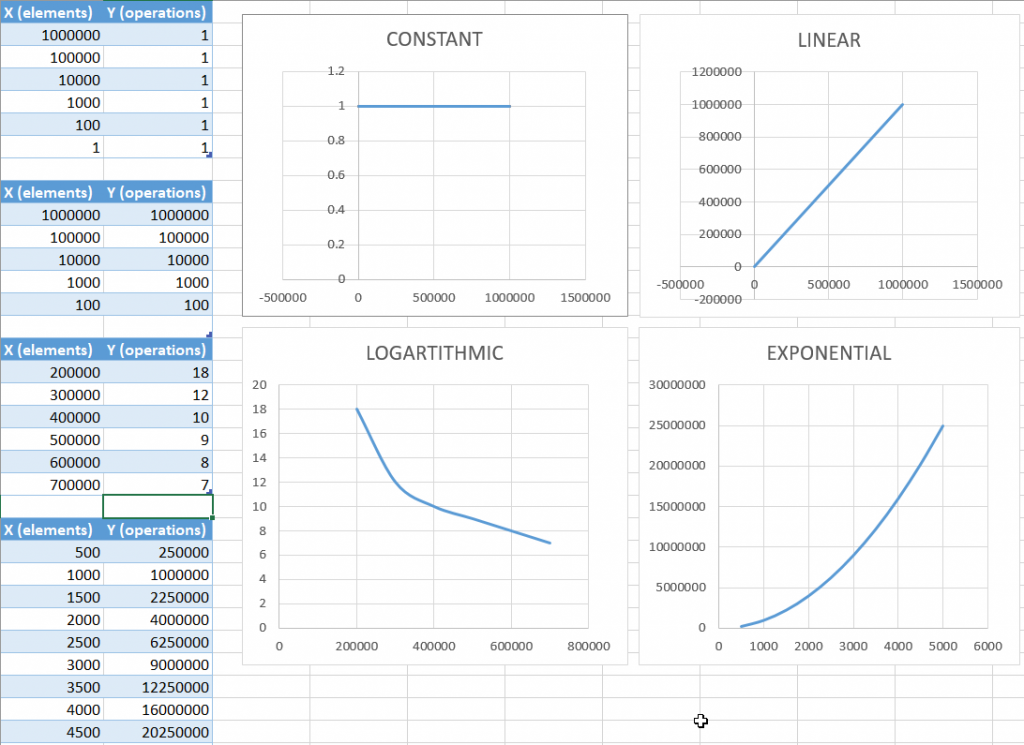
El código completo del programa de consola que hice está disponible en mi cuenta Github, aquí el link 👉 https://github.com/GeaSmart/TimeComplexityDemos.git
Si quieres profundizar en este tema, aquí hay información muy útil de los amigos de Coderbyte, una muy buena web para devs.
Caso práctico (...y muy real)
Ahora ya no te deberían sorprender cuando te pregunten por estos temas, y como regalito, te tengo una pregunta de un exámen técnico real, si haz seguido los ejercicios aquí te será más fácil llegar a la solución, pero igual si tienes dudas aún, pues aquí lo aprenderás, el ejercicio se lo tomaron como parte de una entrevista técnica a un amigo y es el siguiente:

Aplicando los conocimientos ya vistos aquí, notarás que la alternativa A tiene una notación lineal es decir O(n)
La alternativa B tiene una notación lineal pero la mitad de lo que tendría la A ya que aumenta de 2 en 2 entonces su notación sería O(n/2)
La alternativa D nunca termina, ya que al sacar la mitad a un número y repetir sucesivamente nunca terminaremos (debido a la característica infinita de los números reales, siempre es posible sacarle la mitad a un número).
Finalmente la alternativa C tiene una notación logarítmica ya que conforme va avanzando el bucle va haciendo pasos más agigantados porque se va duplicando, como una bola de nieve y por lo tanto realiza menos operaciones, lo que también significa un ahorro en tiempo, entonces su notación sería O(log(n))
Por lo tanto, si te preguntan cuál es la más eficiente, sería la que menos operaciones realiza, y sería la C.
Muy bien crack! ahora ya lo sabes, aprovecha esta valiosa info que está en tus manos y compártela capo en tus redes ya que me ha hecho sufrir un poco y me duele la chimba 😄 hazte una dev.

Si esta entrada te ha gustado crack, compártela! 😉

Un comentario en «Time Complexity o Complejidad temporal: Eficiencia de los algoritmos en términos de tiempo»